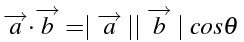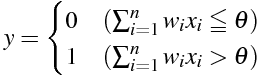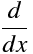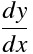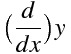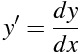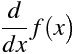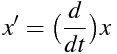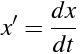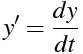iTex2Imgとは?
状態:-
閲覧数:3,383
投稿日:2014-05-15
更新日:2018-02-22
無料でTeX2imgを使用可能なオンラインツール
・会員登録することなくすぐに利用可能
入力したTeXソースコードをTeXでコンパイルして、様々な形式の画像で出力するアプリケーション
・出力する際、フォント指定可能
公式サイト
・Online Latex Equation Editor
・会員登録することなくすぐに利用可能
Convert Latex equations to high resolution images to embed in documents or presentations
入力したTeXソースコードをTeXでコンパイルして、様々な形式の画像で出力するアプリケーション
・出力する際、フォント指定可能
公式サイト
・Online Latex Equation Editor
行列 / 「入力TeXソースコード」+「出力画像」例
設定
Font
・Cmbright
Font Size
・18
行列平行移動数式
\begin{bmatrix}x' \\y' \end{bmatrix} = \begin{bmatrix}x \\y \end{bmatrix} + \begin{bmatrix}tx \\ty \end{bmatrix}
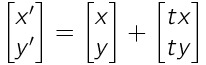
行列拡大縮小数式
LaTeX ソース
~
・改行されない空白
\begin{bmatrix}x' \\y' \end{bmatrix} = \begin{bmatrix}sx~~0 \\0~~sy \end{bmatrix} \begin{bmatrix}x \\y \end{bmatrix}
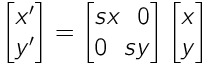
回転
\begin{bmatrix}x' \\y' \end{bmatrix} = \begin{bmatrix} cos \theta ~~-sin\theta\\sin\theta ~~ ~~ cos \theta \end{bmatrix} \begin{bmatrix}x \\y \end{bmatrix}
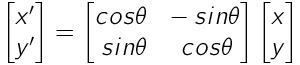
アフィン変換 / 「入力TeXソースコード」+「出力画像」例
設定
Font
・Cmbright
Font Size
・18
汎用的
\begin{bmatrix}x' \\y' \end{bmatrix} = \begin{bmatrix}a~~b \\c~~d \end{bmatrix} \begin{bmatrix}x \\y \end{bmatrix} + \begin{bmatrix}tx \\ty \end{bmatrix}
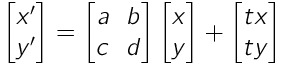
行列乗算
\begin{bmatrix}x' \\y' \\1 \end{bmatrix} = \begin{bmatrix}a~~b~~tx \\c~~d~~ty\\0~~0~~1 \end{bmatrix} \begin{bmatrix}x \\y \\1 \end{bmatrix}
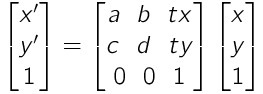
導関数 / 「入力TeXソースコード」+「出力画像」例
設定
Font
・Mathptmx
Font Size
・18
関数f(x)に対する導関数
\lim_{h \to 0} \frac{f(x+h)-f(x)}{h}
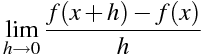
f' (x)=\lim_{h \to 0} \frac{f(x+h)-f(x)}{h}
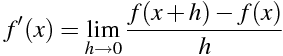
関数 f(x)=x² に対する導関数
\lim_{h \to 0} \frac{f(x+h)-f(x)}{h}=\lim_{h \to 0} \frac{f(x+h) ^{2} -x^{2}}{h} =\ \lim_{h \to 0} \frac{2xh+h ^{2} }{h} ==\ \lim_{h \to 0} (2x+h) } =2x
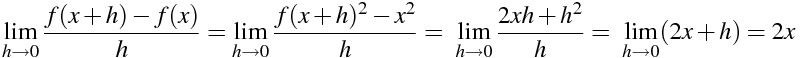
微分係数 / 「入力TeXソースコード」+「出力画像」例
設定
Font
・Mathptmx
Font Size
・18
関数 f(x)の x=aにおける微分係数
f' (a)=\lim_{h \to 0} \frac{f(a+h)-f(a)}{h}
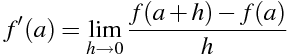
関数 f(x)=x² の x=0における微分係数を計算
\lim_{h \to 0} \frac{f(0+h)-f(0)}{h}=\lim_{h \to 0} \frac{f(0+h) ^{2} -0^{2}}{h} =\ \lim_{h \to 0} \frac{h ^{2} }{h} ==\ \lim_{h \to 0} h } =0
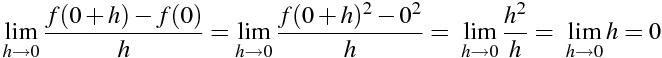
関数 f(x)=x² の x=1における微分係数を計算
\lim_{h \to 0} \frac{f(1+h)-f(1)}{h}=\lim_{h \to 0} \frac{f(1+h) ^{2} -1^{2}}{h} =\ \lim_{h \to 0} \frac{2h+h ^{2} }{h} ==\ \lim_{h \to 0} (2+h) } =2
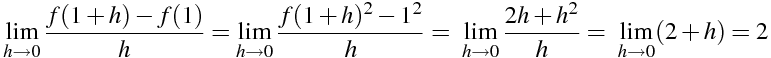
関数 f(x)=x² の x=2における微分係数を計算
\lim_{h \to 0} \frac{f(2+h)-f(2)}{h}=\lim_{h \to 0} \frac{f(2+h) ^{2} -2^{2}}{h} =\ \lim_{h \to 0} \frac{4h+h ^{2} }{h} ==\ \lim_{h \to 0} (4+h) } =4
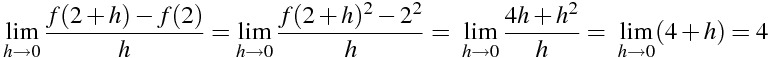
単純パーセプトロン / 「入力TeXソースコード」+「出力画像」例
常微分 / 「入力TeXソースコード」+「出力画像」例
偏微分 / 「入力TeXソースコード」+「出力画像」例
設定
Font
・Mathptmx
Font Size
・18
x³y² を x について偏微分
\frac{\partial}{\partial x} \big( x^{3}y^{2} \big) =3 x^{2} y^{2}
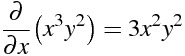
x³y² を y について偏微分
\frac{\partial}{\partial y} \big( x^{3}y^{2} \big) =2 x^{3} y
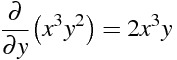
x³y² を z について偏微分
\frac{\partial}{\partial z} \big( x^{3}y^{2} \big) =0
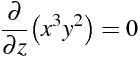
ベクトル / 「入力TeXソースコード」+「出力画像」例
設定
Font
・Mathptmx
Font Size
・18
A から B への向きと、線分 AB の長さを持つベクトル
\overrightarrow{AB}
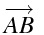
・1つの文字でベクトルを表すこともある
\overrightarrow{AB}=\overrightarrow{b}
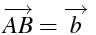
A から C への向きと、線分 AC の長さを持つベクトル
\overrightarrow{AC}
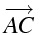
線分 AB の長さ
\mid \overrightarrow{AB}\mid
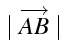
線分 a の長さ
\mid \overrightarrow{a}\mid
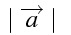
ベクトルの足し算の基本的な考え方
AB, BC というように、しりとりのように足せば、間を取り除いて AC という結論になる
\overrightarrow{AB} + \overrightarrow{BC}=\overrightarrow{AC}
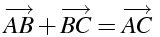
交換法則
足す順番を変えても結果が変わらない
\overrightarrow{a} + \overrightarrow{b}=\overrightarrow{b} + \overrightarrow{a}
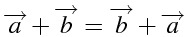
結合法則
どこから足すかを変えても結果が変わらない
(\overrightarrow{a} + \overrightarrow{b})+ \overrightarrow{c}=\overrightarrow{a} + (\overrightarrow{b}+ \overrightarrow{c})
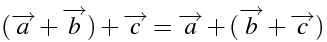
逆ベクトル
- \overrightarrow{AB}
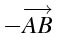
- \overrightarrow{AB} = \overrightarrow{BA}
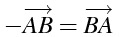
零ベクトル
引き算
\overrightarrow{AB} + \overrightarrow{BA}=\overrightarrow{0}
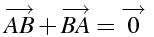
しりとりの形
\overrightarrow{AB} + \overrightarrow{BC}+ \overrightarrow{CA}=\overrightarrow{AC}+ \overrightarrow{CA}=\overrightarrow{AA}=\overrightarrow{0}
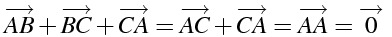
ベクトルの内積
ベクトルaとベクトルbの内積
\mid \overrightarrow{a}\mid
\mid \overrightarrow{b}\mid
cos \theta
\mid \overrightarrow{b}\mid
cos \theta
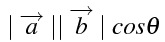
間にある「⋅」を省略できない
・数字の掛け算とも違うので、「⋅」 を「×」 と書いてもいけない
\overrightarrow{a}$\cdot$\overrightarrow{b}
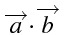
0ベクトル でない2つのベクトaベクトル,bベクトルに対し、なす角をθとする
・このとき、 ベクトaベクトル,bベクトルの内積は、次で定義される
\overrightarrow{a}$\cdot$\overrightarrow{b}=
\mid \overrightarrow{a}\mid
\mid \overrightarrow{b}\mid
cos \theta
\mid \overrightarrow{a}\mid
\mid \overrightarrow{b}\mid
cos \theta