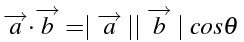カテゴリー:
数学方程式
閲覧数:589 配信日:2018-07-07 11:15
設定
Font
・Mathptmx
Font Size
・18
A から B への向きと、線分 AB の長さを持つベクトル
\overrightarrow{AB}
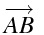
・1つの文字でベクトルを表すこともある
\overrightarrow{AB}=\overrightarrow{b}
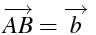
A から C への向きと、線分 AC の長さを持つベクトル
\overrightarrow{AC}
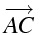
線分 AB の長さ
\mid \overrightarrow{AB}\mid
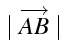
線分 a の長さ
\mid \overrightarrow{a}\mid
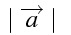
ベクトルの足し算の基本的な考え方
AB, BC というように、しりとりのように足せば、間を取り除いて AC という結論になる
\overrightarrow{AB} + \overrightarrow{BC}=\overrightarrow{AC}
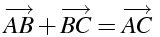
交換法則
足す順番を変えても結果が変わらない
\overrightarrow{a} + \overrightarrow{b}=\overrightarrow{b} + \overrightarrow{a}
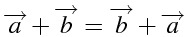
結合法則
どこから足すかを変えても結果が変わらない
(\overrightarrow{a} + \overrightarrow{b})+ \overrightarrow{c}=\overrightarrow{a} + (\overrightarrow{b}+ \overrightarrow{c})
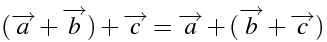
逆ベクトル
- \overrightarrow{AB}
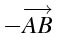
- \overrightarrow{AB} = \overrightarrow{BA}
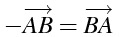
零ベクトル
引き算
\overrightarrow{AB} + \overrightarrow{BA}=\overrightarrow{0}
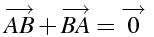
しりとりの形
\overrightarrow{AB} + \overrightarrow{BC}+ \overrightarrow{CA}=\overrightarrow{AC}+ \overrightarrow{CA}=\overrightarrow{AA}=\overrightarrow{0}
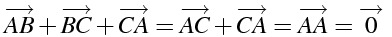
ベクトルの内積
ベクトルaとベクトルbの内積
\mid \overrightarrow{a}\mid
\mid \overrightarrow{b}\mid
cos \theta
\mid \overrightarrow{b}\mid
cos \theta
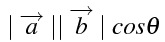
間にある「⋅」を省略できない
・数字の掛け算とも違うので、「⋅」 を「×」 と書いてもいけない
\overrightarrow{a}$\cdot$\overrightarrow{b}
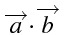
0ベクトル でない2つのベクトaベクトル,bベクトルに対し、なす角をθとする
・このとき、 ベクトaベクトル,bベクトルの内積は、次で定義される
\overrightarrow{a}$\cdot$\overrightarrow{b}=
\mid \overrightarrow{a}\mid
\mid \overrightarrow{b}\mid
cos \theta
\mid \overrightarrow{a}\mid
\mid \overrightarrow{b}\mid
cos \theta