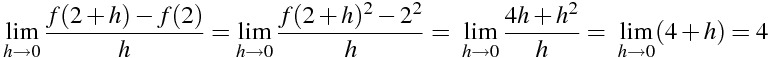カテゴリー:
数学方程式
閲覧数:601 配信日:2018-02-28 11:13
設定
Font
・Mathptmx
Font Size
・18
関数 f(x)の x=aにおける微分係数
f' (a)=\lim_{h \to 0} \frac{f(a+h)-f(a)}{h}
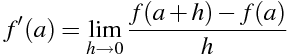
関数 f(x)=x² の x=0における微分係数を計算
\lim_{h \to 0} \frac{f(0+h)-f(0)}{h}=\lim_{h \to 0} \frac{f(0+h) ^{2} -0^{2}}{h} =\ \lim_{h \to 0} \frac{h ^{2} }{h} ==\ \lim_{h \to 0} h } =0
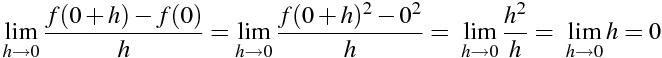
関数 f(x)=x² の x=1における微分係数を計算
\lim_{h \to 0} \frac{f(1+h)-f(1)}{h}=\lim_{h \to 0} \frac{f(1+h) ^{2} -1^{2}}{h} =\ \lim_{h \to 0} \frac{2h+h ^{2} }{h} ==\ \lim_{h \to 0} (2+h) } =2
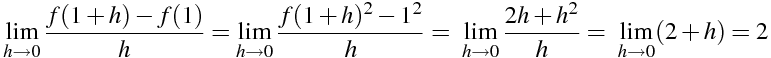
関数 f(x)=x² の x=2における微分係数を計算
\lim_{h \to 0} \frac{f(2+h)-f(2)}{h}=\lim_{h \to 0} \frac{f(2+h) ^{2} -2^{2}}{h} =\ \lim_{h \to 0} \frac{4h+h ^{2} }{h} ==\ \lim_{h \to 0} (4+h) } =4